Fork me on GitHub

第3章数据结构

发表于 | 分类于 | 阅读次数:
字数统计: 3,285 字 | 阅读时长 ≈ 13 分钟

第3章数据结构

线性结构

线性表

栈和队列

串

数组、矩阵和广义表

数组

矩阵

广义表

树

树与二叉树的定义

二叉树的性质与存储结构

二叉树的遍历

线索二叉树

最优二叉树

树和森林

图

图的定义与储存

图的遍历

生成树与最小生成树

拓扑排序和关键路径

最短路径

查找

查找的基本概念

静态查找表的查找方法

动态查找表

哈希表

排序

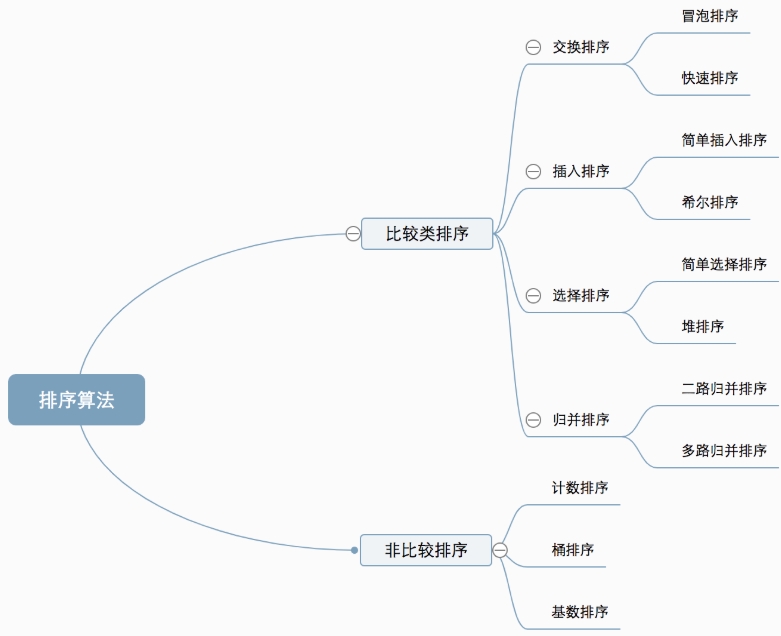
十种常见排序算法可以分为两大类：

比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。

非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

排序的基本概念

假设含 $n$ 个记录文件内容为{$R_{1}, R_{2},\ldots ,R_{n}$}，相应的关键字{$k_{1}, k_{2},\ldots ,k_{n}$}。经过排序确定一种排列{$R_{j_{1}},R_{j_{2}},\ldots ,R_{j_{n}}$}，使得它们的关键字满足以下递增（或递减）关系：$k_{j_1}\leq k_{j_{2}}\leq \ldots \leq k_{j_{n}}$（或$k_{j_{1}}\geq k_{j_{2}}\geq \ldots k_{jn}$）。

若在待排序中的一个序列中，$R_{i}$和$R_{j}$的关键字相同，即 $k_{i}$=$k_{j}$，且在排序前 $R_{i}$先于$R_{j}$，那么在排序后，如果$R_{i}$和$R_{j}$的相对次序保持不变，$R_{i}$仍领先于$R_{j}$，则此类排序算法为稳定的。若在排序后的序列中有可能出现$R_{j}$领先于$R_{i}$的情形，则此类排序为不稳定的。

内部排序：指待排序记录全部存放在内存中进行排序的过程。

外部排序：指待排序记录的数量很大，以至于内存不能容纳全部记录，在排序过程中尚需对外存进行访问的排序过程。

简单排序

直接插入排序

又称简单插入排序，是一种简单的排序算法。

具体做法：在插入第$ i $个记录时，$R_{1}$、$R_{2}$、….、$R_{i-1}$ 已经安排好序，这时将 $R_{i}$的关键字 $k_{i}$依次与 $K_{i-1}$、$K_{i-2}$等进行比较，从而找到应该插入的位置并将$R_{i}$插入，插入位置及其后的记录向后移动。

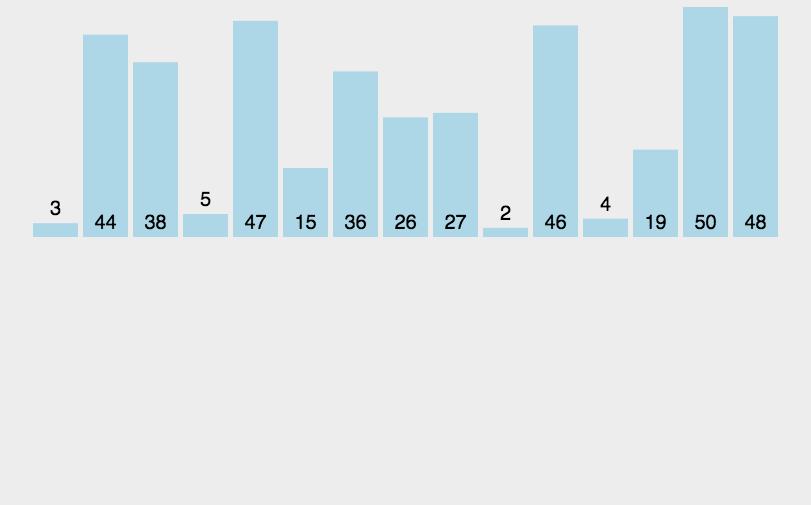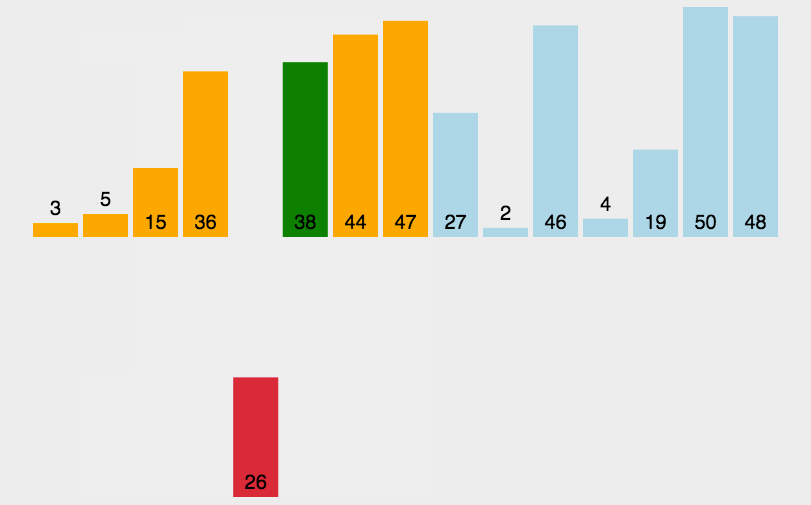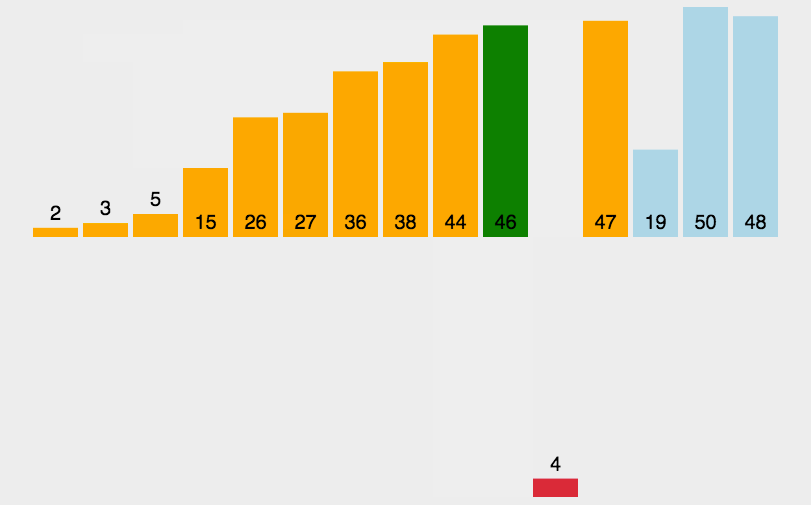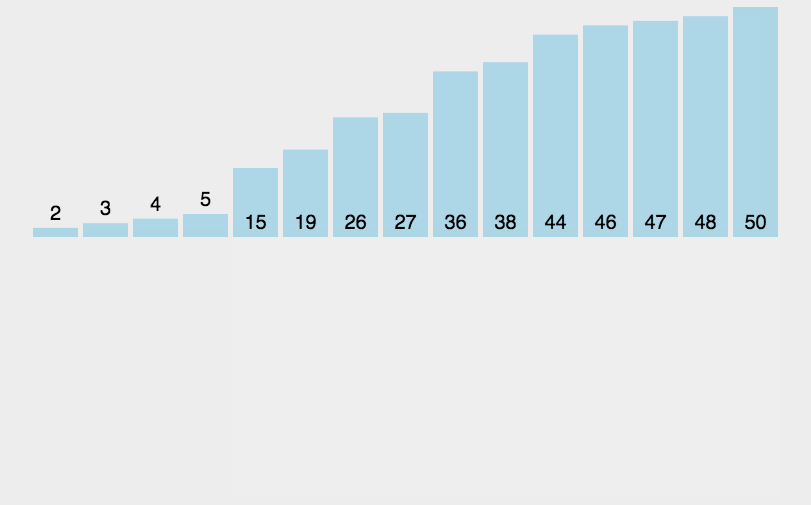
实现程序 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int[] insertionSort(int[] arr){
    int len = arr.length;
    int preIndex,current;
    for(int i = 1;i<len;i++){
        preIndex = i - 1;
        current = arr[i];
        while(preIndex>=0 && current<arr[preIndex]){
            arr[preIndex+1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex+1] = current;
    }
    return arr;
}

直接排序算法在最好的情况下（待排序列已按关键码有序），每趟只需操作 1 次比较且不需要移动元素，因此$n$个元素排序时的总比较次数为$ n-1$ 次，总移动次数为0。在最坏情况下（元素已经逆序排序），进行第 $i$ 趟排序时，待插入的记录需要同前面的 $i$ 个记录进行比较，因此，总比较次数为 $\dfrac {n\left( n-1\right) }{2}$在排序过程中，第 $i$ 趟排序时移动记录的次数为 $i+1$ （包括移进、移除tmp）,总移动次数为 $\dfrac {\left( n+3\right) \left( n+2\right) }{2}$

注意：是一种稳定的排序算法;时间复杂度$O\left( n^{2}\right)$;在排序过程中仅需要一个元素的辅助空间用于交换，空间复杂度为$O\left( 1\right)$

冒泡排序

一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

具体的做法：

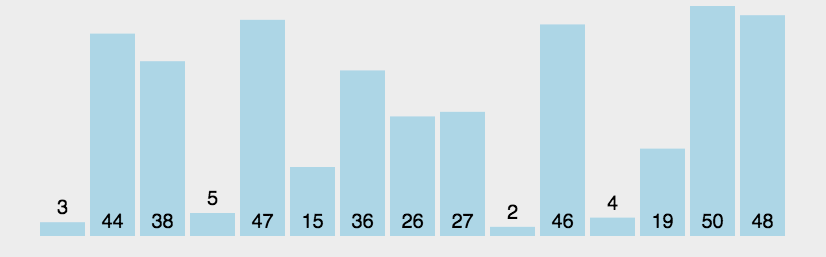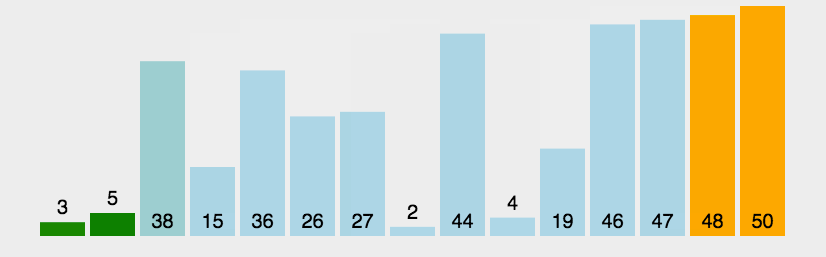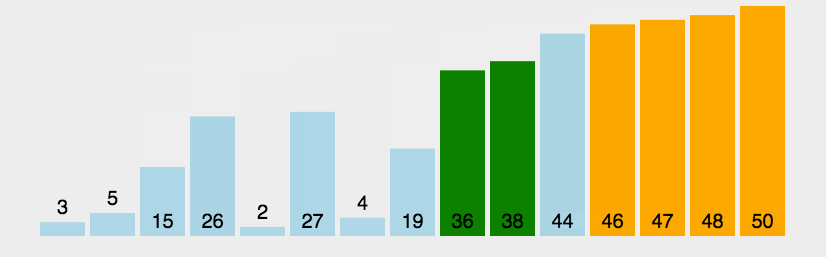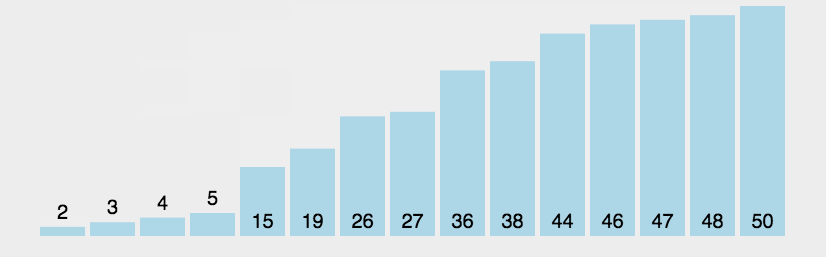
实现程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
public int[] bubbleSort(int[] arr){
    int n = arr.length;
    for(int i = 0;i < n - 1;i++){
        for(int j = 0 ; j < n - 1 - i;j++){
            if(arr[j]>arr[j+1]){
                int temp = arr[j+1];
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

冒泡排序在最好情况下（待排序列已按关键码有序），只需要做一趟，元素的比较次数为 $n-1$ 且不需要交换元素。在最坏情况下（元素已经逆序排序），在进行第 $j$ 趟排序时，最大的 $j-1$ 个元素已经排好序，其余的 $n-(j-1)$ 个元素需要进行 $n-j$ 次比较和 $n-j$ 次交换。因此总比较次数为：$\dfrac {n\left( n-1\right) }{2}$ ，总的交换次数为：$\dfrac {n\left( n-1\right) }{2}$

注意：稳定的排序方法；时间复杂度$O\left( n^{2}\right)$;在排序过程中仅需要一个元素的辅助空间用于交换，空间复杂度为$O\left( 1\right)$

简单选择排序

是一种简单直观的排序算法。工作原理：首先在末尾排序序列中找到最小（大）元素，存放到排序序列的其实位置，然后，再从剩下元素中继续寻找最小（最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

具体做法：

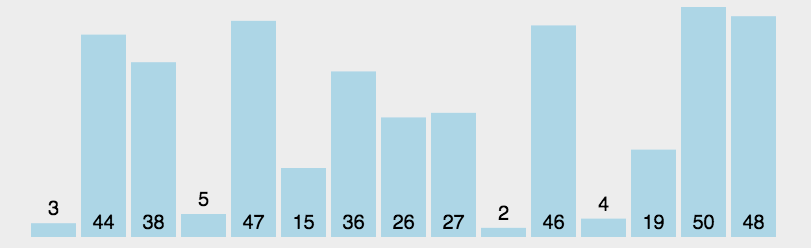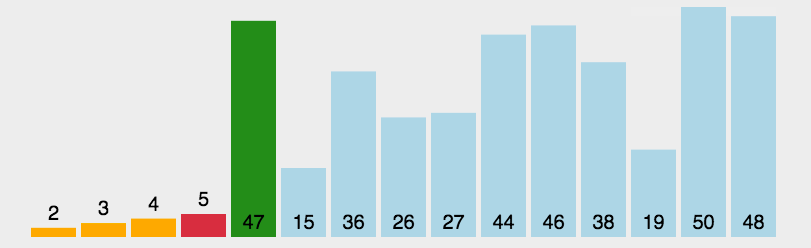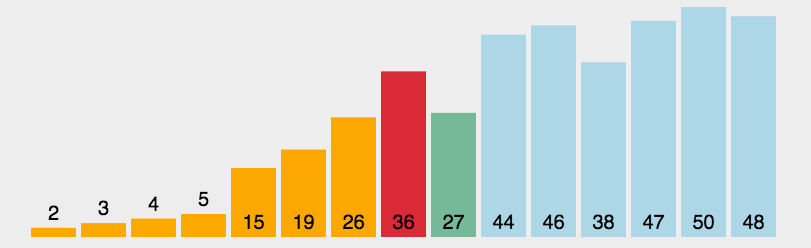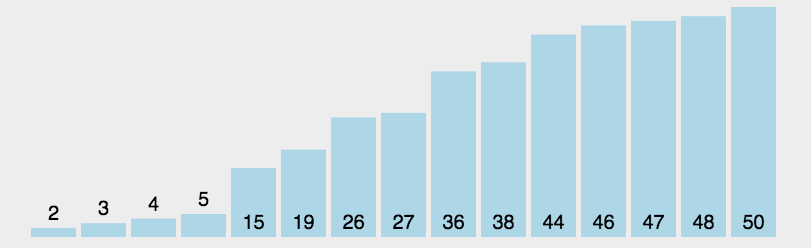
程序实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int[] selectionSort(int[] arr){
    int n = arr.length;
    int minIndex,temp;
    for(int i = 0;i < n;i++){
        minIndex = i;
        for(int j = i+1;j<n;j++){
            if(arr[j]<arr[minIndex]){
                minIndex = j;
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

简单选择排序算法在最好情况下（待排序列按关键码有序），不需要移动元素，因此 n 个元素排序时的总移动次数为 0 次。在坏情况下（元素已经逆序排序），前$\dfrac {n}{2}$趟中，每趟排序移动记录的次数都为3次（两个数组元素加交换值），其后不再移动元素，共进行 n-1 趟排序，总移动次数为$3\left( n-1\right) /2$。无论哪种情况，元素总比较次数为$\dfrac {n\left( n-1\right) }{2}$。

注意：不稳定的排序方法；时间复杂度为：$O\left( n^{2}\right)$；在排序过程中仅需要一个元素的辅助空间用于数组元素的交换，空间复杂度为$O\left( 1\right)$

希尔排序

是第一个突破$O\left( n^{2}\right)$的排序算法，是简单插入排序的改进版。与插入排序的不同之处在于，它会优先比较距离较远的元素，通过逐步减少间距，最终以1为间距或者进行一次常规的插入排序。希尔排序又叫缩小增量排序。

具体做法：先取一个小于 n 的整数 d1 作为第一个增量，把文件的全部记录分成 d1 个组，即将所有距离为 d1 倍数序号的记录放在同一个组中，在和组内进行直接插入排序；然后取第二个增量 d2（d2<d1），重复上述分组和排序工作，依次类推，直到所有的增量 d = 1，即所有的记录放在同一组进行直接插入排序为止。

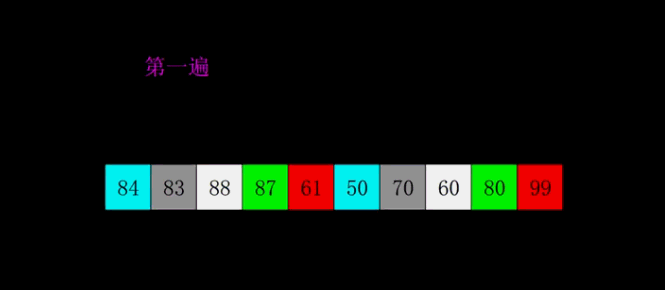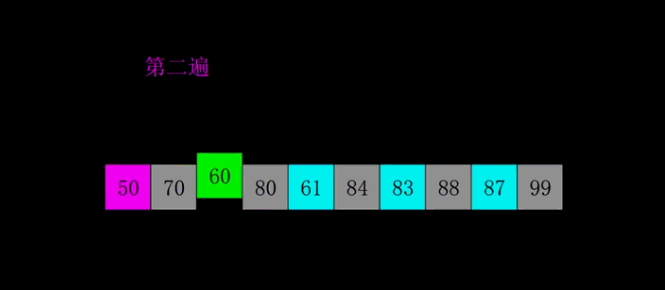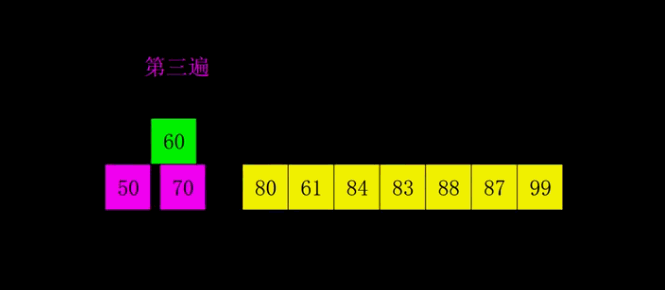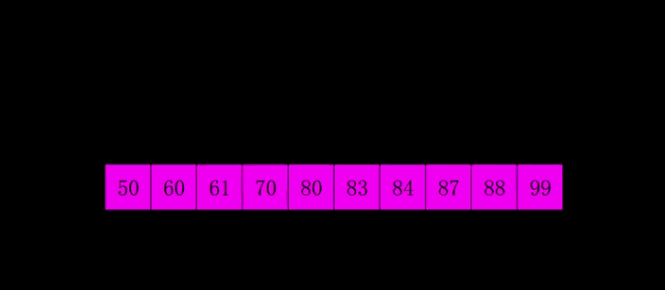
程序实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int[] shellSort(int[] arr){
    int n = arr.length;
    for(int gap = (int)Math.floor(n/2);gap > 0;gap = (int)Math.floor(gap/2)){
        for(int i = gap;i < n;i++){
            int j = i;
            int current = arr[i];
            while(j - gap >= 0 && current < arr[j - gap]){
                arr[j] = arr[j - gap];
                j = j - gap;
            }
            arr[j] = current;
        }
    }
    return arr;
}

注意：是一种不稳定的排序方法；时间复杂度为：$O\left( n^{1.3}\right)$；空间复杂度数为：$O\left( 1\right)$

快速排序

基本思想：通过一趟排序将待排序的记录划分为独立的两部分，称为前半区和后半区，其中，前半区中记录的关键字均不大于后半区记录的关键字，然后再分别对这两部分记录继续进行快速排序，从而使整个序列有序。

一趟快速排的过程称为一次划分，具体的做法是：设两个位置指示变量 i 和 j，它们的初始值分别指向序列的第一个记录和最后一个记录。设枢轴记录（通常是第一个记录）的关键字为 pivot,则首先从 j 所指定的位置向前搜索，找到第一个关键字小于 pivot 的记录时向前移到 i 的位置，然后从 i 所指位置向后搜索，找到第一个关键字大于 pivot 的记录时将改记录向后移到 j 所指位置，重复该过程直至 i 与 j 相等位置。

具体做法：

请看 https://swenfang.github.io/2019/03/30/SoftTestTechnique/快速排序原理和实现/#more 这篇文章。

程序实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class QuickSort{
    
    public static void main(String[] args) {
        int[] arr = {6,1,2,7,9,3,4,5,10,8};
        quickSort(arr,0,arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    // 划分
    private static int partition(int arr[],int low,int high){
        // 用 arr[low] 作为枢纽轴元素 pivot 进行划分
        // 使得 arr[low,...,i-1] 均不大于 pivot，data[i+1,...,high]均小于 pivot
        int i,j; int pivot;
        pivot = arr[low]; i = low;j = high;
        while(i < j){
            /*从数组的两端交替地向中间扫描*/
            while(i < j && arr[j] >= pivot)j--;
            arr[i] = arr[j];/*比枢轴元素小者往前移动*/
            while(i < j && arr[i] <= pivot)i++;
            arr[j] = arr[i];/*比枢轴元素大者往后移动*/
        }
        arr[i] = pivot;
        return i;
    }
    // 对整型数组进行非递减排序
    private static int[] quickSort(int arr[],int low,int high){
        if(low<high){
            int loc = partition(arr,low,high);/*进行划分*/
            quickSort(arr,low,loc-1);/*对前半区进行快速排序*/
            quickSort(arr,loc+1,high);/*对后半区进行快速排序*/
        }
        return arr;
    }
    
}

注意：快速排序算法的时间复杂度为 $O\left( n\log _{2}n\right)$，在所有算法复杂度为此数量级的排序方法中，快速排序被认为是平均性能最好的一种。但是，若初始记录序列按关键字有序或基本有序时，即每次划分都是将序列分为某一半序列的长度为0的情况，此时快速排序的性能退化为时间复杂度是$O\left( n^{2}\right)$。快速排序是一种不稳定的排序算法。

堆排序

归并排序

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

具体做法：

程序实现：

递归法（Top-down）

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
  4. 重复步骤3直到某一指针到达序列尾
  5. 将另一个序列剩下的所有元素直接复制到合并序列尾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class MergeSort{
    public static void main(String[] args){
        int[] arr = {6,1,2,7,9,3,4,5,10,8};
        sort(arr,0,arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
    // 使用递归
    public static void Sort(int[] arr,int leftStart,int rightEnd){
        // 满足基本条件
        if(leftStart>=rightEnd){
            return;
        }
        // 算出左边数组结束位置
        int leftEnd = (leftStart+rightEnd) >> 1;
        // 算出右边数组开始位置
        int rightStart = leftEnd+1;
        /*递归地对arr[leftStart...leftEnd]进行归并排序*/
        Sort(arr,leftStart,leftEnd);
       /*递归地对arr[rightStart...rightEnd]进行归并排序*/
        Sort(arr,rightStart,rightEnd);
        /*对一维数组arr[leftStart...rightEnd]中的元素进行两路归并牌排序*/
        Merge(arr,leftStart,leftEnd,rightStart,rightEnd);
    }
    
    // 两两归并
    public static Merge(int[] arr,int leftStart,int leftEnd,int rightStart,int rightEnd){
        // 定义一个临时数组
        int[] tempArr = new int[arr.length];
        int tempIndex = leftStart;
        int resultIndex = leftStart;
        // 进行比较
        while(leftStart <= leftEnd && rightStart <= rightEnd){
            tempArr[tempIndex++] = arr[leftStart] <= arr[rightStart] ? 	                                       arr[leftStart++]:arr[rightStart++];
        }
        // 把最后一个比较的元素存放到临时素组中
        while(leftStart<=leftEnd){
            tempArr[tempIndex++] = arr[leftStart++];
        }
        while(rightStart <= rightEnd){
             tempArr[tempIndex++] = arr[rightStart++];
        }
        
        // 把临时数组元素顺序复制到原数组
        while(resultIndex <= rightEnd){
            arr[resultIndex] = tempArr[resultIndex++]
        }
    }
}

迭代法（Bottom-up）

假设序列共有 n 个元素

  1. 将序列每相邻两个数字进行归并操作，形成 floor(n/2)个序列，排序后每个序列包含两/一个元素
  2. 若此时序列数不是1个则将上述序列再次归并，形成 floor(n/4)，每个序列包含四/三个元素
  3. 重复步骤2，直到所有元素排序完毕，即序列数为1
1
2

适用：多链表排序。

基数排序

内部排序方法小结

外部排序

坚持原创技术分享，您的支持将鼓励我继续创作！